Variance in programming languages

Covariance, invariance, and contravariance are concepts many students have difficulties to grasp. However, the idea behind them is pretty simple. This post will attempt to illustrate that in a shortest and simplest way possible.

Take an imaginary object-oriented language with generic types. Java or C# will do. We are going to draw diagrams, where rectangles represent types and arrows represent a relation "is parent of".

A \(\rightarrow\) B means "A is a parent of B", or, in other words, "A is a supertype of B".

Let's create two hierarchies:

Now we will draw a 3x3 matrix with all possible substitutions of x, y and z as type parameters of A<T>, B<T> and C<T>, like this:

two-hierarchies.png

You already see the arrows like A<x> \(\rightarrow\) B<x>; these are not going anywhere, they are valid for any value of type argument.

What is of interest to us is: for a parameterized type such as A, how will A<x> and A<y> be related?

There can be three cases:

Invariance
whatever relation exists between x and y, A<x> and A<y> have no relation whatsoever.
Covariance
if x \(\rightarrow\) y, then A<x> \(\rightarrow\) A<y>.
Contravariance
if x \(\leftarrow\) y, then A<x> \(\rightarrow\) A<y>.
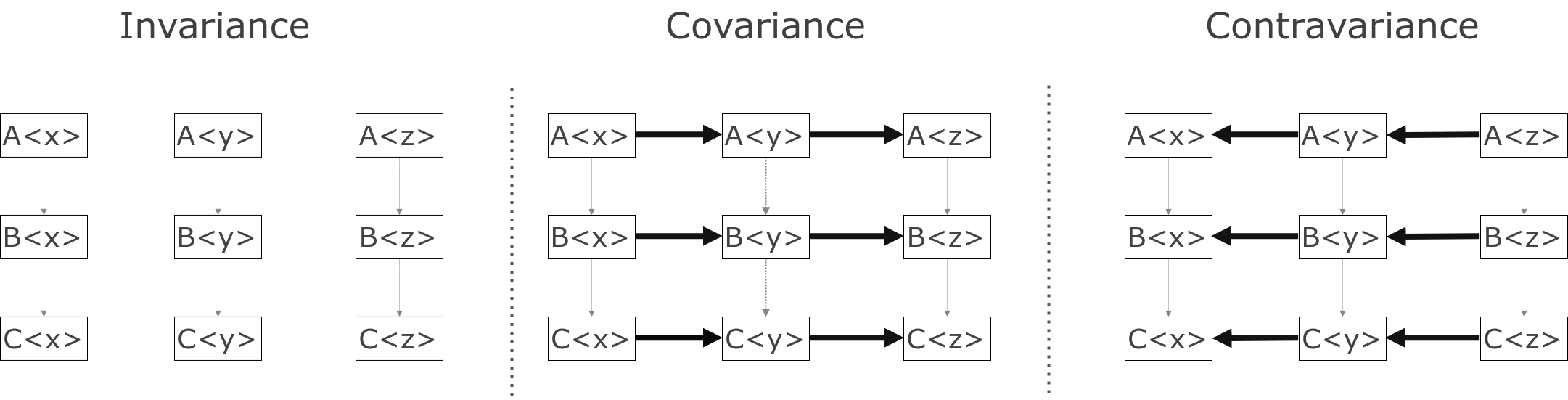
three.png

It's all on the picture: for invariance, A<x> and A<y> are not connected for x \(\neq\) y; for covariance, we draw more arrows according to the hierarchy of type arguments themselves; for contravariance, we invert these arrows.

Language prerequisites

In order for variance to even exist we need the language to have the following features:

  • It has to be typed

  • It should sometimes allow an entity of type A to be implicitly interpreted as an entity of type B.

    The most common cases are:

    • Subtyping in class hierarchies.

      Basically, everything that has an "Object Oriented Programming" label on it: C++, C#, Java etc.

    • Implicit type conversions (coercions).

      For example, in C/C++/Java, there are implicit conversions from numeric types into their wider versions, like short to long, or float to double.

  • We also need parameterized types.

    It does not mean a presence of generics though, as functions alone are enough to introduce covariance and contravariance.

In other words, we need to be able to represent types as an oriented graph.

Common facts

Here I want to mention a couple of facts it is useful to be aware of.

Function variance

Functions are contravariant on arguments and covariant on return type. Why so?

  • A function that returns a Cat can be used to fill a variable of type Animal. Hence we got the "natural" way: Animal is more generic than Cat, function returning Animal is more generic than function returning Cat.
  • If you need a function that can work on Cat (its argument), it is safe to use a function that can work on Animal instead, or any supertype of Cat. Hence, the function with a more generic argument type is of a more specific type itself.

Variance and mutability

As a rule of thumb, immutable collections can be covariant, mutable collections should be invariant.

Imagine, that a mutable List is covariant. Then take a List<String>. You can reinterpret it as a List<Object>, because Object \(\rightarrow\) String. That list can store anything, so it is a valid operation to add an integer to it. From the type perspective, its method set (int idx, T value) will become set(int idx, Object value), so it is valid to give it an integer as a value. If we do it, we are screwed because we just have added an integer to a list that assumes it is holding strings, the objects of an incompatible type, effectively hacking the type system.

The next time when we try to use some function like printString on all elements of the said list, we are up for some surprises, ranging (depending on the language semantics) from runtime errors, to undefined behavior.

In Scala, if you try to define a covariant List, you will get warned on the definition of its set method, that accepts an argument of type T (corresponding to the list contents). As an argument of set, T should be contravariant (as in any function), but as a type parameter of List, it will be marked as covariant (because we made it so in List definition). Hence the warning: "Covariant argument in contravariant position".

Immutable collections do not have such problem. If we try to replicate that example, we will just get a new List of objects, for which it is perfectly fine to store everything you might want it to.