Putting a bigger sphere inside a smaller one
Can we put a sphere with a bigger radius inside of a smaller one so that it would be fully contained? The answer is yes, but we have to select the space we are working in carefully. I am going to provide two examples here:
First example: metric space
Suppose we are in a metric space with Euclidean metric. The space is a sphere itself, with radius \(r\). Let us denote a closed sphere of radius \(r\) with center at 0 as \(D_r(0)\). This sphere is a subset of \(R^n\).
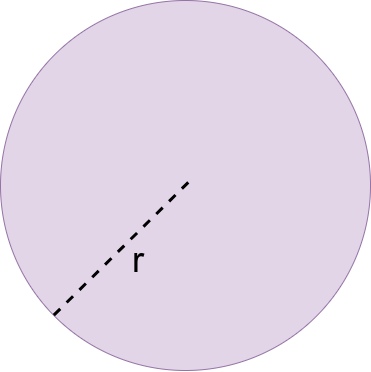
What is a sphere? By definition it is a point of a space and a set of such points that are no further than the sphere's radius. What if we try to define a sphere of radius \(R > r\) inside the space we are working in?
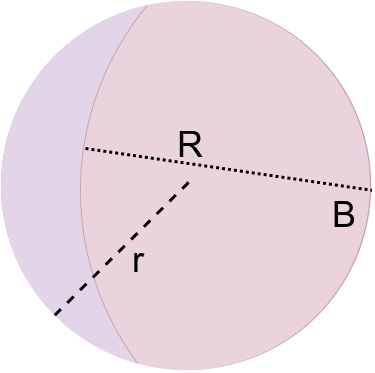
Why does this sphere look as an intersection of two? We are, by definition, effectively selecting a subset of points of space \(D_r(0)\) whose distance to \(B\) is less or equal to \(r\). Any point of \(R^n\) lying outside of \(D_r(0)\) is out of reach.
As long as \(R < 2r\), we can fit a bigger sphere inside of a smaller one. Once we cross the \(2r\) border, even if we pick a center \(B\) on the border of the \(D_r(0)\), the longest distance between two points inside of \(D_r(0)\) can not surpass \(2r\). Thus, all points will be contained inside of \(D_R(B)\).
Second example
We can also pick up a less traditional kind of space, for example, a graph. Let us label its edges with numbers and take the shortest path as a metric.
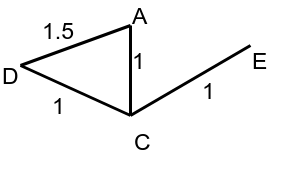
It is easy to see that \(D_{1.5}(D) \subset D_{1}(C)\), for:
\[D_{1.5}(D) = \{ D, A, C\}\]
\[D_{1}(C) = \{C, D, A, E\}\]