Memory in CompCert: overview
CompCert is a certified C compiler written in Coq. I work with it to create a verified refactorer, that is proven correct w.r.t. operational semantics of C. During my journey, I am tackling various parts of CompCert, including its memory model. It might seem interesting, how they dealt with raw memory and handled things like encoding values.
There were several versions of memory specification. This note is describing the second version, as of CompCert 2.6. Some minor details are omitted for brevity (like alignment checks); I will probably make more posts about memory and connected subjects. But first we have to take a look at Radix trees, a data structure pervasive in CompCert.
Radix (Patricia) trees in CompCert
Radix tree is a data structure to implement partial mapping from integers. It is extensively used to implement all sorts of maps, such as:
- Memory: maps block IDs into block contents
- Memory block: maps offsets into block elements.
- Symbol table: maps global symbol IDs into memory blocks.
- Environment: maps local symbol IDs into pairs of block ID and symbol type.
The type is defined in CompCert in lib.Maps.PTree:
Inductive tree (A : Type) : Type := | Leaf : tree A | Node : tree A -> option A -> tree A -> tree A
A node with no children (a leaf in terms of trees) is encoded as Node Leaf val Leaf. Nodes can store values or be empty. The latter is useful because in Radix trees the paths themselves matter.
Positive integers in Coq
Positive integers are represented through their binary encoding:
Inductive positive : Set :=
| xI : positive -> positive
| xO : positive -> positive
| xH : positive
Since positive integers always start with leading one, we are using xH to
encode it. Applying xO appends zero, applying xI appends one. The result
looks like the binary representation of a number written from right to left.
For example, an integer number 11 is represented as 1011 in binary form. The
corresponding term in Coq will be:
xI (xI (xO xH) )
Paths are positive integers
There is an isomorphism between positive integers and paths in PTrees.
All paths in PTree start at root, just like positive integers start as xH. Then
they either go to the left or to the right, which corresponds to the choice
between applying xO or xI.
Encoding maps using Radix trees
Radix trees are used to encode partial maps from positive integers into some domain. The domain values are stored into nodes; the path to the node corresponds to its index.
Let us encode a map:
\[\begin{cases}% 1 \mapsto \text{"one"}\\ 3 \mapsto \text{"three"}\\ 4 \mapsto \text{"four"} \end{cases}\]
As a tree, it will look like this:
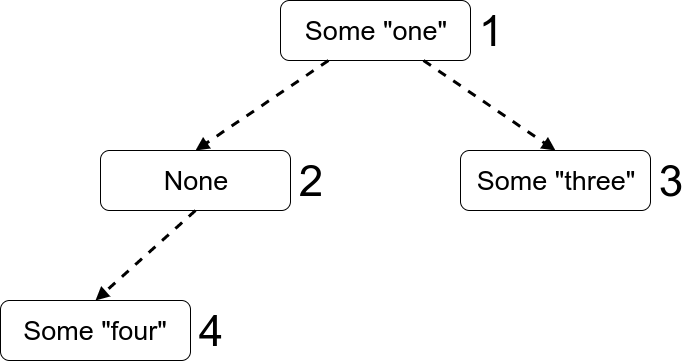
As we see, the elements are enumerated according to the breadth-first search order.
Other tree-related types
PTreeis a type of a Radix/Patricia tree;PTree.getreturnsNoneif no element has a given index.PMapis a pair ofPTreeand a default value returned byPMap.getinstead ofNoneZMapisPMapwhere any integer can be used instead of only positive ones. It is done through a bijection between all integers and positive integers.
Memory: basic notions
Memory is a mapping of addresses into block contents coupled with permissions map and some constraints.
*Block contents/ maps offsets (integers) into memory values.
All pointers are pairs of block index and an offset inside a block, so it is impossible to jump from one block into another by changing the offset value. In other words, blocks can not overlap by design.
Value
Values are encoded as follows:
Inductive val : Type :=
Vundef : val
| Vint : Int.int -> val
| Vlong : Int64.int -> val
| Vfloat : Floats.float -> val
| Vsingle : Floats.float32 -> val
| Vptr : block -> Int.int -> val
Memory value
Memory value is defined as follows:
Inductive memval : Type :=
Undef : memval
| Byte : int -> memval
| Fragment : val -> quantity -> nat -> memval
Such memory values are assigned to addresses, which means that a block of \(n\) bytes holds \(n\) such values.
Undefis used to mark the cell as uninitialized. All reads involving such
cells are resulted in Vundef value returned.
Byteis a concrete 8-bit integer. It is also a type of raw memory. Such raw
values can be taken in a pack and decoded in an architecture-dependent way using decode_val.
Fragmentis a usual case of storing data. It contains an opaque value, a quantity and an index, showing where exactly are we in this value.
Additional arguments include:
- A quantity is either
Q32orQ64. 8-byte values have quantity set toQ64, the other ones areQ32. - An offset in ranges 0..3 or 0..7. As each element of a block represents a single byte, we are storing as many consecutive
Fragmentsas there are bytes in a value. EachFragmentstores its index w.r.t. the value's beginning address.
Note The source [1] states that only pointers are stored inside fragments, while other values are split into bytes according to the architecture specification. The lemmas however never impose such restriction, making cases like Fragment (Vint 4%Z) _ _ possible by construction (and appear in proofs).
For example, executing this assignment:
int32_t x; int32_t* px; ... px = &x
results in the following values being written into memory (assuming x inhabits in the block #4 and a pointer is 32 bits wide).
(Fragment ((Vptr 4 0) Q32 0) :: (Fragment ((Vptr 4 0) Q32 1) :: (Fragment ((Vptr 4 0) Q32 2) :: (Fragment ((Vptr 4 0) Q32 3) :: nil
Permissions
Every address has two associated permissions (access rights) . They put constraints on which operations with are allowed on it.
Permissions are shown in the table below:
| Permission | Read | Write | Free |
|---|---|---|---|
| Freeable | + | + | + |
| Writable | + | + | |
| Readable | + | ||
| Nonempty |
Non-allocated and freed cells can have None as permissions.
The first permission value associated with a memory byte is its maximal permission: it is set on allocation and can be lowered during execution using drop_perm operation.
The current permission is varying between Nonempty and maximal permission.
Operations on memory
Memory itself is not opaque and we can have easily access to the inner tree structure of its contents. However, all memory-related lemmas defined in CompCert rely on specifically crafted memory operations. These are opaque and can not be unfolded into their exact definitions. For us it means that we can only prove our own theorems based on such properties of these transformations, that are already proven in CompCert.
alloc : mem -> Z -> Z -> mem * block free : mem -> block -> Z -> Z -> option mem load : memory_chunk -> mem -> block -> Z -> option val store : memory_chunk -> mem -> block -> Z -> val -> option mem loadbytes : mem -> block -> Z -> Z -> option (list memval) storebytes : mem -> block -> Z -> list memval -> option mem drop_perm : mem -> block -> Z -> Z -> permission -> option mem
Note For now, we are only going to study load, store, loadbytes and storebytes operations.
loadaccepts a chunk type (Mint32,=Mint8signed= etc.), source memory, block ID and offset. It returns a decoded value orNone.storeaccepts a chunk type (Mint32,=Mint8signed= etc.), source memory, block ID and offset, and a value. It returns an instance of memory with overwritten cells orNone.loadbytesaccepts source memory, block ID and offset, and the amount of bytes to load. It returns a list of memory values orNonestorebytesaccepts source memory, block ID and offset and a lit of memory values. It returns an instance of memory with overwritten cells orNone.
There are lemmas that allow reasoning about load results involving:
- Previous
storeresult loadbytesextendsandinjectionunchanged_ondecode_valwith a direct memory access.
The following lemma allows us to get raw contents from memory and decode them using decode_val
load_result:
forall (chunk : memory_chunk) (m : mem) (b : block) (ofs : Z) (v : val),
load chunk m b ofs = Some v ->
v = decode_val chunk
(getN (size_chunk_nat chunk) ofs (PMap.get b (mem_contents m)))
Memory: implementation
Memory is represented as a record:
Record mem' : Type := mkmem
{ mem_contents : PMap.t (ZMap.t Memdata.memval);
mem_access : PMap.t (Z -> perm_kind -> option permission);
nextblock : Values.block;
access_max : forall (b : positive) (ofs : Z),
perm_order'' (PMap.get b mem_access ofs Max)
(PMap.get b mem_access ofs Memtype.Cur);
nextblock_noaccess : forall (b : positive) (ofs : Z) (k : perm_kind),
~ Plt b nextblock -> PMap.get b mem_access ofs k = None;
contents_default : forall b : positive,
fst (PMap.get b mem_contents) = Undef }
All mappings are implemented as Patricia Trees.
mem_contentsmaps block IDs (positive integers) into block contents. It is a map implemented on top of a Radix tree. Block contents are maps from offsets (integers, possibly negative) into block elements.mem_accessmaps block IDs into functions, which accept an offset, a permission type (MaxorCur) and return the actual permissions for this block.nextblockis the maximal block ID. All blocks with ids in range from 1 inclusive tonextblockexclusive should exist.access_maxencodes the following property: for all blocks their maximal permissions are higher than their current permissions.nextblock_noaccessencodes the following property: no block has an ID greater or equal tonextblockcontents_defaultencodes the following property: for all blocks the default memory cell value isUndef.
Useful sources
- "Program Logic for Certified Compilers". Chapter 32 "The CompCert memory model"